Towers of Hanoi

A "Divide-and-Conquer" Algorithm

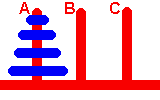
The Towers of Hanoi is a classic problem where you try to move all of the discs on one peg to another peg using only three pegs. Initially, all of the discs are stacked on top of each other with the larger discs under the smaller discs. You may move a disc to any of the three pegs as you attempt to relocate all of the discs, but you can not place a larger disc over a smaller disc.

This problem can be easily solved with a recursive "divide-and-conquer" algorithm. Here's how it works:

Assume you have n discs located on peg A (the pegs are labeled A, B, and C from left to right). Think of solving the problem by moving n-1 discs from peg A to peg C, moving the nth disc from peg A to peg B, and then moving the n-1 discs from peg C to peg B.

The program for solving this problem would be:

void hanoi(char From, char To, char Other, int n)
{
    if (n == 0) return;

    hanoi(From, Other, To, n-1);

    printf("Moving disc from peg %c to %c\n", From, To);

    hanoi(Other, To, From, n-1);
}

void main()
{
    // Last parameter represents the number of discs
    hanoi('A','B','C', 4);
}

The output of the program (which moves 4 discs) would be:

Moving disc from peg A to C
Moving disc from peg A to B
Moving disc from peg C to B
Moving disc from peg A to C
Moving disc from peg B to A
Moving disc from peg B to C
Moving disc from peg A to C
Moving disc from peg A to B
Moving disc from peg C to B
Moving disc from peg C to A
Moving disc from peg B to A
Moving disc from peg C to B
Moving disc from peg A to C
Moving disc from peg A to B
Moving disc from peg C to B